题目

题目描述

每一头牛的愿望就是变成一头最受欢迎的牛。现在有N头牛，给你M对整数(A,B)，表示牛A认为牛B受欢迎。这种关系是具有传递性的，如果A认为B受欢迎，B认为C受欢迎，那么牛A也认为牛C受欢迎。你的任务是求出有多少头牛被所有的牛认为是受欢迎的。

输入

第一行两个数N,M。接下来M行，每行两个数A,B，意思是A认为B是受欢迎的（给出的信息有可能重复，即有可能出现多个A,B）

输出

一个数，即有多少头牛被所有的牛认为是受欢迎的。

样例输入

样例输出

提示

100%的数据N<=10000,M<=50000

题解

虽然网上有不少题解，但我觉得还是自己写下，毕竟题解这东西首先是写给自己的。

缩点分析

假如你已经完全搞懂了tarjan的话可以直接看这里。
当我们把所有的强连通分量分别合并到一个点里（每次标记出栈的点，这些点就在同一个强连通分量里），不难发现，统计每一个点的出度，如果有1个点出度为0，那么这个点里的所有牛就是最受欢迎的了，其他情况则没有最受欢迎的牛，如图：

tarjan算法

tarjan算法用来寻找有向图的强连通分量的算法，它可以在$ O(|V|+|E|) $ 的时间内得出结果。下面内容大部分来源于这篇文章。

为了更好地理解tarjan算法是如何通过dfs来求强连通分量的，我们这里不妨先了解下搜索树。
比如这是一个有向图：

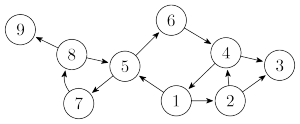
而他的搜索树长这样：

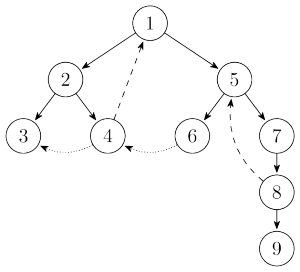
从图中我们可以看到3种边（实际上有4种，但是其实第四种只要和第一种一样处理就可以了）

1.实线画出来的是树边，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
2.用长虚线画出来的是反祖边，也被叫做回边,它主要是在搜索的时候遇到了一个已经访问过的结点，而且这个结点是当前节点的祖先时形成的。
3.用短虚线画出来的是横叉边，它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点不是当前节点的祖先时形成的。

现在我们来看看在 DFS 的过程中强连通分量有什么性质。

很重要的一点是如果结点 u 是某个强连通分量在搜索树中遇到的第一个结点（这通常被称为这个强连通分量的根），那么这个强连通分量的其余结点肯定是在搜索树中以 u 为根的子树中。如果有个结点 v 在该强连通分量中但是不在以 u 为根的子树中，那么 u 到 v 的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边，然而这两条边都要求指向的结点已经被访问过了，这就和 u 是第一个访问的结点矛盾了。

Tarjan 算法主要是在 DFS 的过程中维护了一些信息：dfn、low 和一个栈。

栈里的元素表示的是当前已经访问过但是没有被归类到任一强连通分量的结点。

dfn[u] 表示结点 u 在 DFS 中第一次搜索到的次序，通常被叫做时间戳。

low[u] 稍微有些复杂，它表示从 u 或者以 u 为根的子树中的结点，再通过一条反祖边或者横叉边可以到达的时间戳最小的结点 v 的时间戳，并且要求 v 有一些额外的性质：v 还要能够到达 u。显然通过反祖边到达的结点 v 满足 low 的性质，但是通过横叉边到达的却不一定。
可以证明，结点 u 是某个强连通分量的根等价于 dfn[u] 和 low[u] 相等。简单可以理解成当它们相等的时候就不可能从 u 通过子树再经过其它时间戳比它小的结点回到 u。

当通过 u 搜索到一个新节点 v 的时候可以有多种情况：

$ 1° $ 结点 u 通过树边到达结点 v
$$ low[u]=min(low[u],low[v]) $$

$ 2° $ 结点 u 通过反祖边到达结点 v，或者通过横叉边到达结点 v 并且满足 low 定义中 v 的性质
$$ low[u]=min(low[u],dfn[v]) $$

如果 dfn 和 low 相等，那么就不断退栈直到当前结点为止，这些结点就属于一个强连通分量。

至于如何更新 low，关键就在于第二种情况，当通过反祖边或者横叉边走到一个结点的时候，只需要判断这个结点是否在栈中，如果在就用它的 low 值更新当前节点的 low 值，否则就不更新。因为如果不在栈中这个结点就已经确定在某个强连通分量中了，不可能回到 u。

附：链式前向星

代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define MAXN 50001

int E[MAXN],low[MAXN],Next[MAXN],Head[MAXN],dfn[MAXN],num=0,count,out[MAXN],o,how_many[MAXN],chudu[MAXN],zhan[MAXN],top=0;
bool v[MAXN],chuzhan[MAXN];

void add(int x,int y,int i){
	E[i]=y;
	Next[i]=Head[x];
	Head[x]=i;
}

int find(){
	int ans=0;
	for(int i=1;i<=o;i++){
		for(int p=Head[out[i]];p;p=Next[p]){
			if(!chuzhan[E[p]]){
				ans++;
			}
		}
	}
	return ans;
}

void tarjan(int u){
	dfn[u]=low[u]=++num;
	zhan[++top]=u;
	v[u]=1;
	for(int p=Head[u];p;p=Next[p]){
		int y=E[p];
		if(!dfn[y]){
			tarjan(y);
			low[u]=min(low[y],low[u]);
		}else{
			if(v[y])low[u]=min(low[u],dfn[y]);
		}
	}
	if(dfn[u]==low[u]){
		int y;
		count++;
		do{
			y=zhan[top--];
			v[y]=0;
			out[++o]=y;
			chuzhan[y]=1;
			how_many[count]++;
		}while(y!=u);
		chudu[count]=find();
		o=0;
		memset(chuzhan,0,sizeof(chuzhan));
	}
}

int main(){
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y,i);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i])tarjan(i);
	}
	int c=0,ans;
	for(int i=1;i<=count;i++){
		if(!chudu[i])c++,ans=i;
	}
	if(c==1)cout<<how_many[ans];
	else cout<<"0";
	return 0;
}

题目